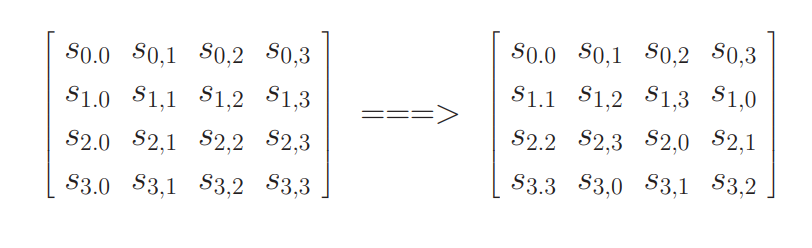Post

Blockchain Chapter 1 Basics

Posted Updated
Preview Image
By Harsh Gharsandiya
9 min read
Blockchain Chapter 1 Basics

1. Basics

  1. Centralized vs Decentralized vs Distributed
  2. Blockchain
  3. Generic Elements of a Blockchain
  4. Hash Function
  5. Merkle Tree
  6. Blockchain Properties & Limitations
  7. Sidechain
  8. Cryptography
  9. Symmetric
  10. MAC
  11. Hash
  12. DES
  13. AES
  14. PKC
  15. Distributed Hash Tables
  16. Digital Signature
  17. RSA
  18. RSA DSA
  19. Elliptic Curve
  20. Elliptic Curve DSA
  21. Zero Knowledge Proofs
  22. Distributed File Systems
  23. Hadoop DFS
  24. Turing Complete
  25. ASIC Resistant

Centralized vs. Decentralized vs. Distributed Systems

FeaturesCentralized SystemDecentralized SystemDistributed Systems
ControlSingle authorityMultiple coordinatorsNo central authority
Failure ToleranceLow (Single Point of failure)Moderate (Few failures tolerated)High (No single point of failure)
ScalabilityLowModerateHigh
MaintenanceLowModerateDifficult
SpeedFastModerateSlow
SecurityLowModerateHigh
DevelopmentEasyModerateComplex
EvolutionSlowFastVery Fast

Blockchain

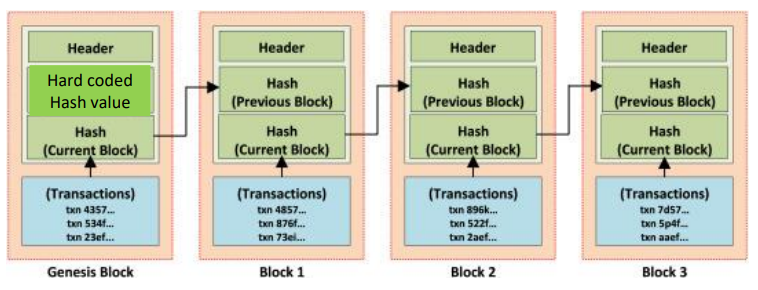
  • It is a distributed ledger with growing lists of records (blocks) that are securely linked together via cryptographic hashes.
  • Each block contains a cryptographic hash of the previous block, a timestamp, and transaction data
  • Blockchain ensures synchronization of information within a finite time interval.
  • It is a decentralized database that enables multiple nodes to communicate without a central authority.
  • Each node maintains a local copy of the global ledger, ensuring consistency and preventing reliance on a single entity.
  • Data on the blockchain is tamper-proof, verifiable, and persistent.
  • It acts as a public ledger, storing historical information for future computation.
  • Example: In banking, historical transactions are stored and used to validate new transactions.

Properties of Blockchain

  1. Decentralization – No single entity has control over the network.
  2. Distributed Ledger – Data is replicated across multiple nodes for reliability.
  3. Consensus Mechanism – Ensures all participants agree on the validity of transactions.
  4. Security & Immutability – Cryptographic techniques prevent data tampering.
  5. Transparency & Auditability – Transactions are publicly recorded and verifiable.
  6. Disintermediation – Eliminates the need for third-party intermediaries.
  7. Irrefutability – Digitally signed transactions cannot be denied or reversed.
  8. Permanence – Once recorded, transactions cannot be modified or deleted.
  9. Network Resilience – Redundancy across nodes ensures system robustness.
  10. Fault Tolerance – Can maintain security even with a fraction of malicious participants.
  11. Guaranteed Transaction Inclusion – Valid transactions are always processed.
  12. Censorship Resistance – No entity can restrict participation in the network.
  13. High Availability – Continuous operation without downtime.
  14. Robust Security – Advanced cryptographic protocols safeguard data integrity.

Limitations of Blockchain

  1. Scalability – Slow transaction processing and high resource usage.
  2. Adoption – Requires broader industry acceptance.
  3. Regulation – Unclear legal frameworks.
  4. Immaturity – Still developing with technical challenges.
  5. Privacy – Transparency may conflict with confidentiality.

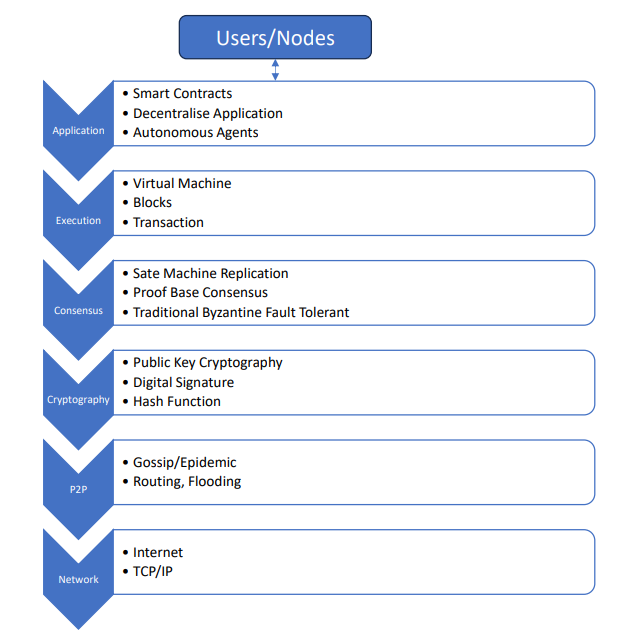
Architecture of Generic Blockchain

image.png

Generic Elements of a Blockchain

  • Block is composed of
    1. Transactions (Block Body) : Record of an event.
    2. Hash of Previous block
    3. Time stamp : Creation time of block
    4. Nonce : Use only once number provide replay protection, authentication and encryption
    5. Merkle root : hash of all the nodes of a Merkle tree.
  • Genesis Block: The first block in a blockchain, hardcoded at the start.

image.png

image.png

Hash Functions

  • Maps data of arbitrary length to a fixed-size output.
  • Trivial hash function → H(x) = x mod n
  • Fixed-size hash also known as digest/checksum
  • Ensures data integrity.
  • Examples:
    • SHA family: SHA1 (SHA160), SHA256, SHA512
    • RIPEMD family: RIPEMD160, RIPEMD256
  • Security level (e.g., SHA160 needs 2^160 steps to break; reduced to 2^80 by the birthday paradox).

Requirements for Secure Hash Functions

  1. Preimage Resistance (One-wayness)
    • Given x, we can compute H(x), but from H(x), we cannot determine x.
  2. Second Preimage Resistance (Weak Collision Resistance)
    • Given x1 and H(x1), finding x2 such that H(x1) == H(x2) is difficult.
  3. Collision Resistance (Strong Collision Resistance)
    • Finding two different inputs (x1 ≠ x2) that produce the same hash is computationally hard.
  4. Avalanche Effect
    • A small change in input leads to a significant change in hash output.

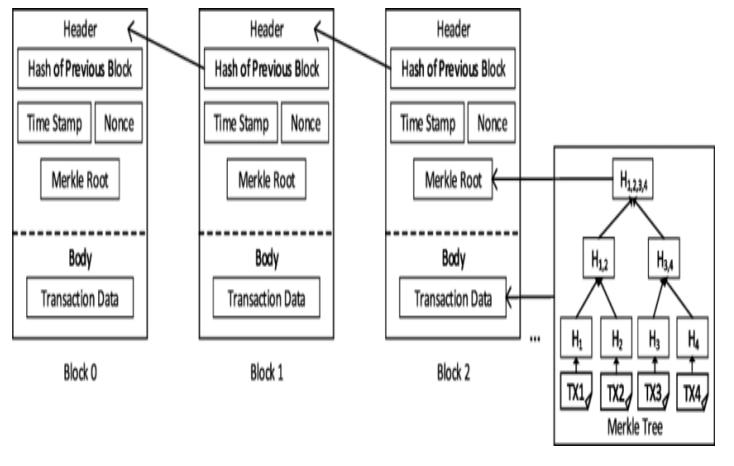
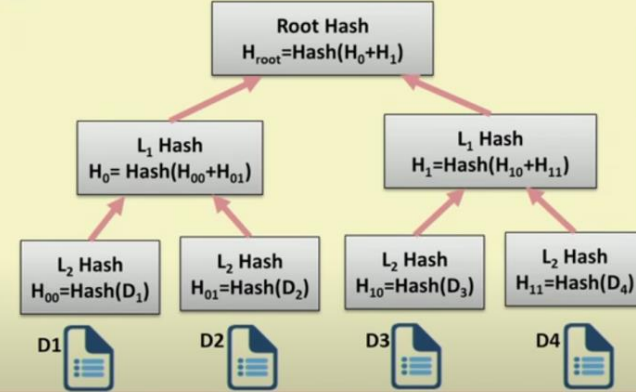
Merkle Tree

  • Structure:
    • Leaf nodes → Contain hashes of data blocks.
    • Non-leaf nodes → Contain hashes of their child nodes.
  • Functionality:
    • Used to secure multiple documents (e.g., D1, D2, D3, D4).
    • Any change in a document alters the root hash, ensuring integrity.
  • Applications:
    • Data integrity in Peer-to-Peer (P2P) Networks → Ensures received data blocks are unaltered.
    • Bitcoin implementation → Ensures shared transaction data remains unmodified and trustworthy.

    image.png

Sidechain

  • Sidechains are smaller blockchains that run parallel to the mainchain, enhancing functionality and efficiency.
  • Sidechains rely on the mainchain, but the mainchain operates independently.
  • Allow transfer of token movement between the mainchain and sidechain.
  • Token from one blockchain can be used in the sidechain and vice versa called pegged sidechain because supports two-way pegged assets.
  • Coins are burned as proof of stake, validating transactions. (Proof of Burn)

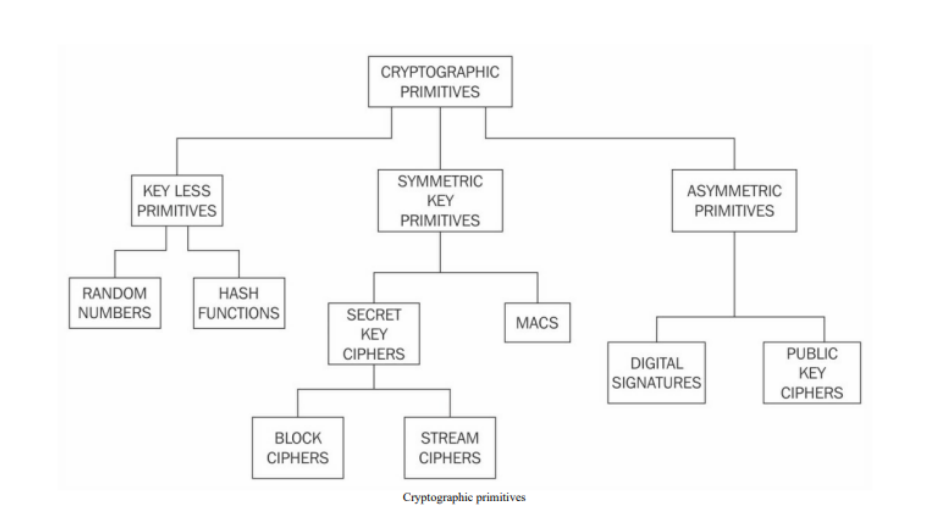
Cryptography

CIAAN Model

  1. Confidentiality – Ensures data is accessible only to authorized users.
  2. Integrity – Guarantees data remains unaltered and trustworthy.
  3. Availability – Ensures data and systems are accessible when needed.
  4. Authentication – Verifies the identity of users and devices.
  5. Non-repudiation – Prevents denial of actions or transactions by involved parties.

Types

image.png

Symmetric

  • Uses a single key for both encryption and decryption.
  • Share Key / Secret Key
  • Faster than asymmetric but require secure key exchange.

Types of Symmetric

  1. Stream Ciphers – Encrypt data bit-by-bit.
  2. Block Ciphers – Encrypt data in fixed-size blocks.

Stream Ciphers

  • Process data one bit at a time.
  • Types:
    1. Synchronous Stream Ciphers – Keystream depends only on the key.
    2. Asynchronous Stream Ciphers – Keystream depends on key + encrypted data.
  • Security depends on randomness of the keystream.
  • Examples: RC4, A5

Block Ciphers

  • Encrypts fixed-length blocks of data.
  • Uses substitution-permutation networks (SPN) and Feistel structures.
  • Key Concepts:
    1. Confusion (Substitution) – Make relationship between plaintext and ciphertext complex (via S-boxes).
    2. Diffusion (Transposition) – Spreads plaintext statistically over ciphertext.
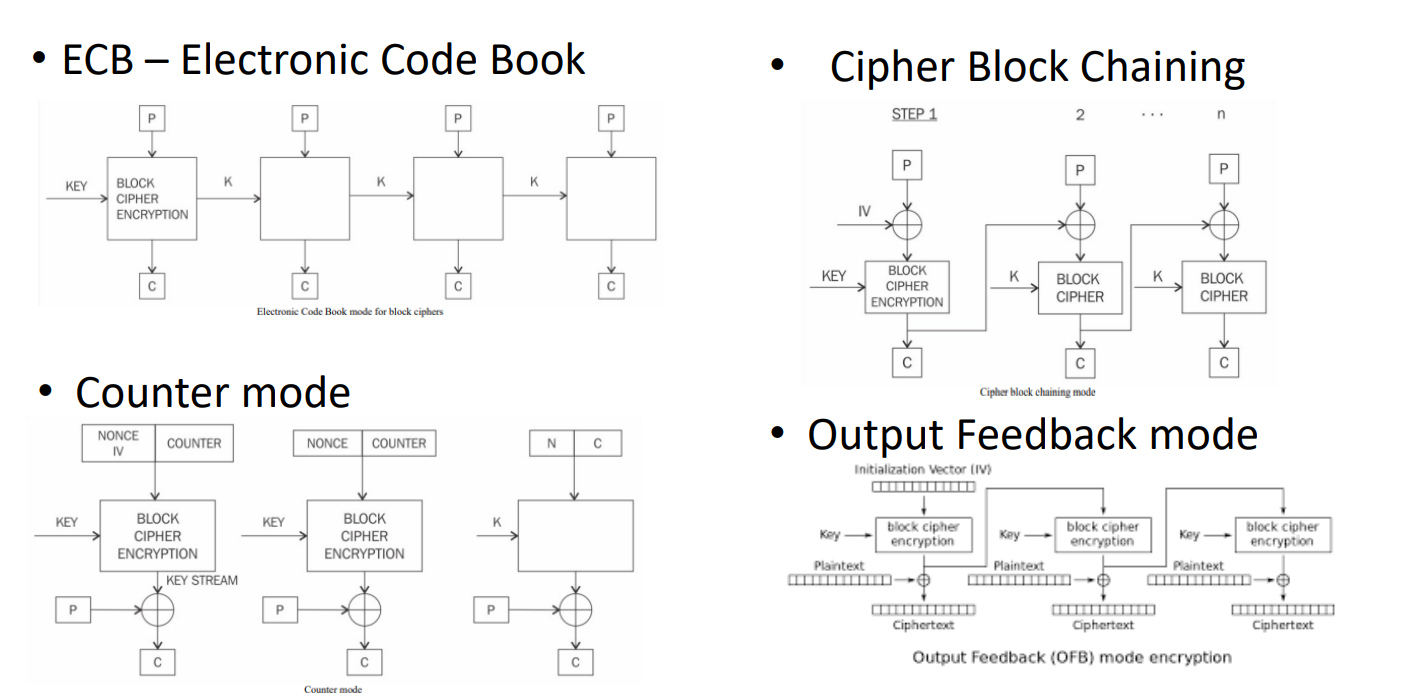
  • Modes of Operation:
    1. ECB (Electronic Code Book)
    2. CBC (Cipher Block Chaining)
    3. OFB (Output Feedback)
    4. CTR (Counter Mode)
  • Examples: DES, AES

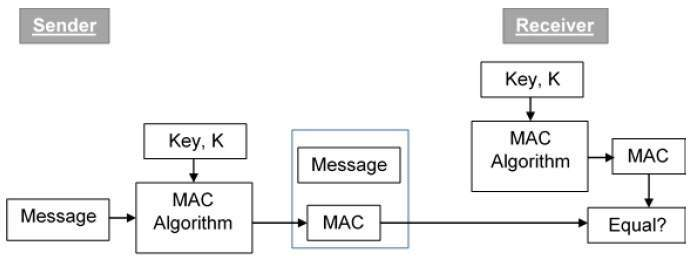
image.png

MAC

  • Message Authentication Code
  • Generated using a secret key and the message.
  • A cryptographic checksum used to verify message integrity and authenticity.

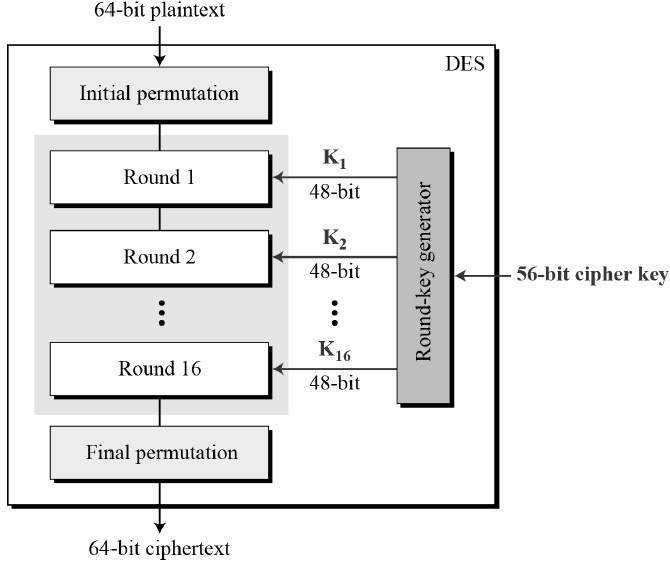
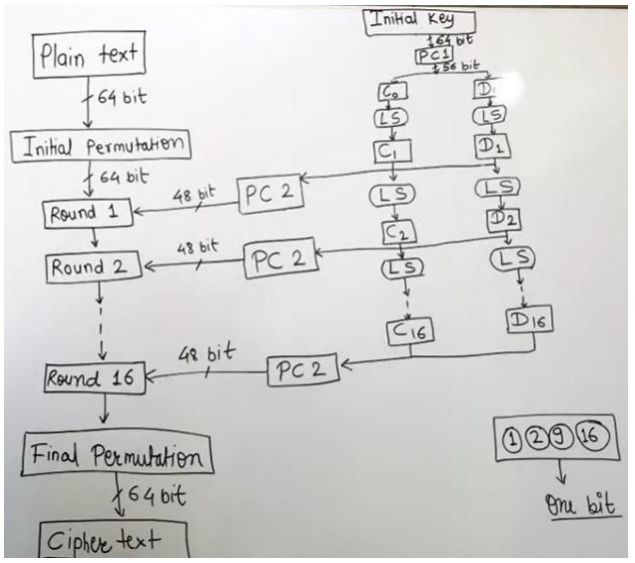
image.png

Data Encryption Standard (DES)

  • Block size: 64 bits.
  • Key size: 64 bits, but effective key length is 56 bits (8 bits used as parity checks).
  • Based on the Feistel Cipher structure with 16 rounds of encryption.

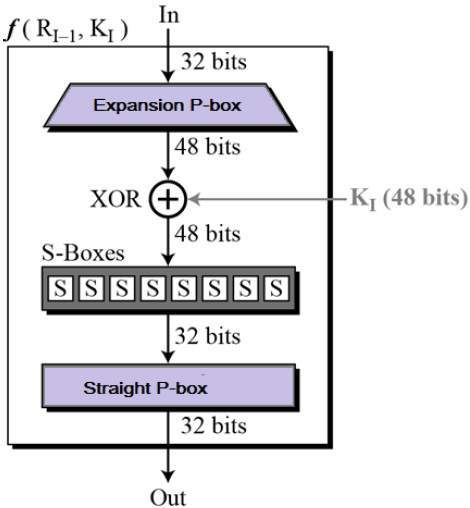
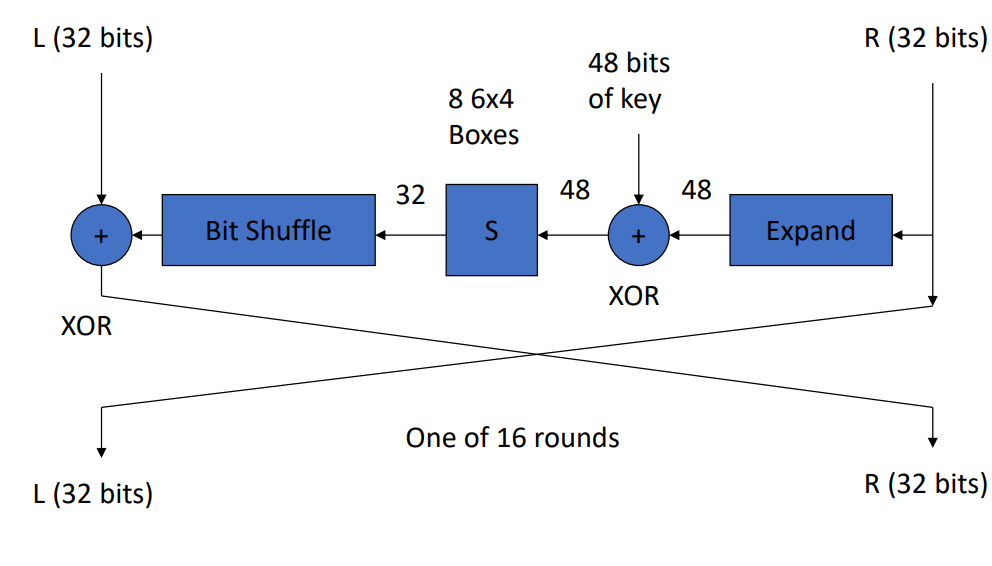
image.png

image.png

Round Function

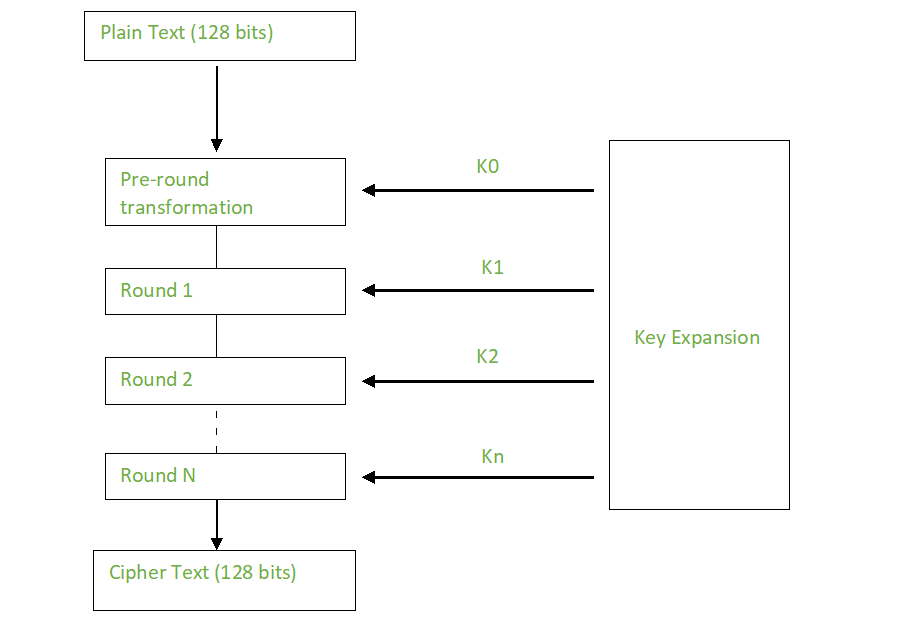
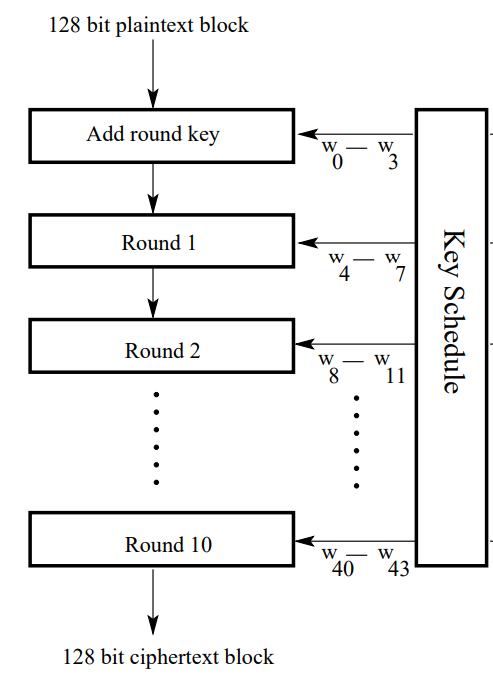
image.png

image.png

Advanced Encryption Standard (AES)

  • Block Size : 128 bits
(Number of Rounds)Key Size (in bits)
10128
12192
14256
  • Cryptocurrency wallets use AES to encrypt locally-stored data.

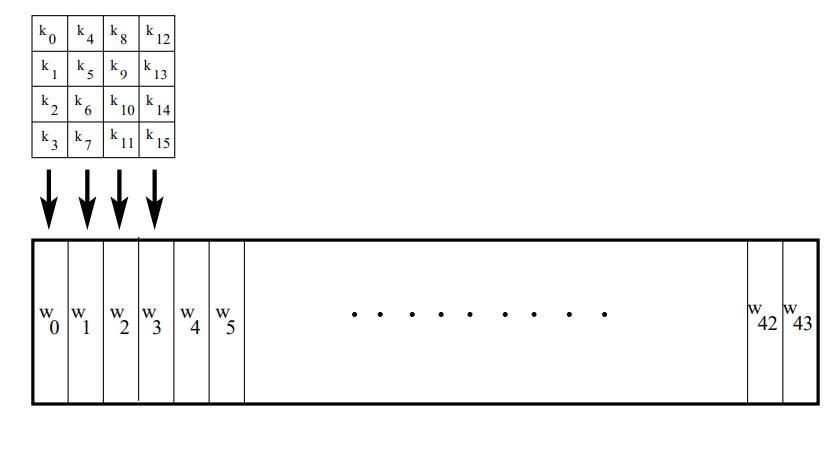
Creation of Round Keys

image.png

Encryption

  • 128 bit = 16 byte (4x4)
b0b4b8b12
b1b5b9b13
b2b6b10b14
b3b7b11b15

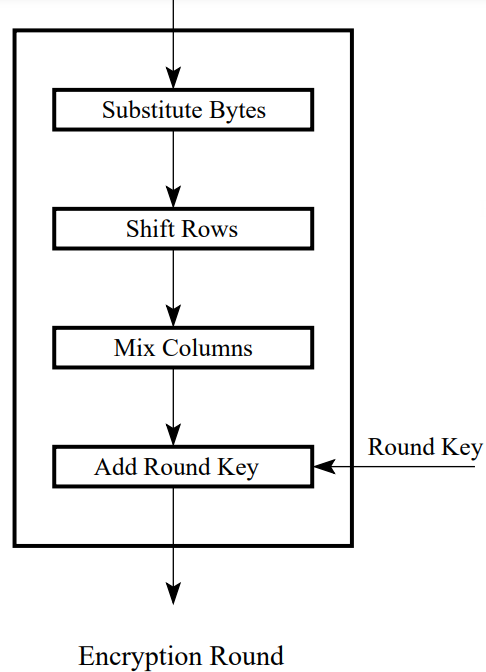
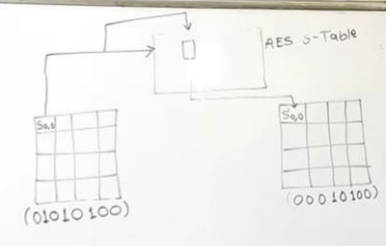
image.png

Substitute Bytes

  • 1,8 = Row
  • 2 to 7 = Column

image.png

Key Expansion

image.png

Shift Rows

image.png

Mix Columns

image.png

Structure of AES

image.png

Public Key Cryptography

  • Also known as asymmetric cryptography.
  • Uses two keys:
    • Public key (shared openly).
    • Private key (kept secret).

Algorithm:

  • RSA – Based on integer factorization.
  • DSA – Used for digital signatures.
  • ElGamal – Based on discrete logarithms.
  • ECC (Elliptic Curve Cryptography) – Uses elliptic curve mathematics for security.

Application:

  1. Encryption & Decryption
  2. Digital Signatures
  3. Key Exchange
  4. Authentication

Mathematical Basics:

  1. Integer Factorization – Hard to factorize large numbers (RSA).
  2. Discrete Logarithm – Difficult to compute reverse operations in modular arithmetic (ElGamal).
  3. Elliptic Curves – Based on the complexity of solving logarithms over elliptic curves (ECDSA, ECDH).

image.png

Distributed Hash Tables

  • Decentralized storage system that maps keys to values efficiently.
  • Uses a hash function to determine the location of data in a network.
  • Data is stored in buckets using hash keys and organized systematically.
  • Commonly used in P2P networks, distributed databases, file systems, and content delivery networks.
  • Advantages: Scalable, efficient, fault-tolerant, decentralized, and secure.
  • Disadvantages: Complexity, potential security risks, performance issues, compatibility challenges, and limited functionality.
  • Popular DHT algorithms: Chord, Kademlia, Pastry.
  • Ensures fault tolerance by distributing copies of data across multiple nodes.
  • Supports fast lookups without requiring a central authority.

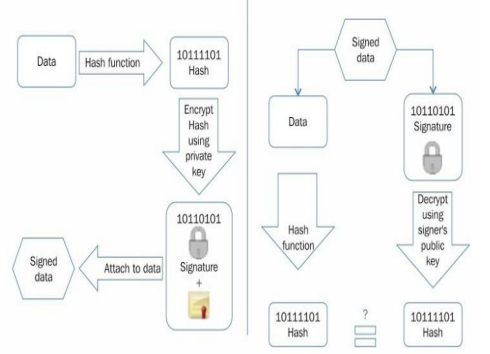
Digital Signature

  • Verifies ownership and integrity using cryptographic keys.
  • Used in blockchain to sign and verify transactions.
  • Ensures authentication and non-repudiation.
  • Common algorithms: RSA, DSA, ECDSA.

RSA Key Generation

  1. Modulus Generation:
    • Pick two large prime numbers p and q.
    • Compute modulus
    \[n = p×q\]
  • Choose a Co-Prime e:
    • Pick e such that
    \[1 < e < (p-1)(q-1)\]
    • e must be co-prime to (p−1)(q−1) (i.e., no common factors except 1).
  • Public Key:
    • (n,e) is the public key (can be shared).
    • Keep p and q secret.
  • Private Key Calculation:
    • Compute private key d using:
    \[d = e^{-1} \mod (p-1)(q-1)\]

    • This means

      \[(e×d)mod(p−1)(q−1)=1.\]
  • Encryption & Decryption:
    • Encryption:
    \[C = P^e mod\ n\]

    • Decryption:

      \[P = C^d mod\ n\]

RSA Digital Signature Algorithm

image.png

Elliptic Curve Cryptography

  • Uses the equations:

    \[y^2 = x^3 + ax + b\]
  • More secure with smaller keys (e.g., 256-bit ECC ≈ 3072-bit RSA).
  • Used in ECDH (Elliptic Curve Diffie-Hellman) for key exchange.
  • Used in ECDSA (Elliptic Curve Digital Signature Algorithm) for digital signatures.
  • Operations:
    1. Point Addition: Adds two different points.
    2. Point Doubling: Adds a point to itself.

ECDSA

  • Private Key (sk): A randomly generated integer used for signing.
  • Public Key (pk):
\[pk = sk \ * \ G\]

where G is the generator point on elliptic curve.

  • Signature (r, s): Two integers generated during the signing process.

Signing

\[r = k \ * \ G\] \[s = k^{-1}(H(M) \ + \ r.sk\]

Verification

\[c = s^{-1} (mod \ N)\] \[u1 = H(M) \ c \ (mod \ N)\] \[u2 = r.c \ (mod \ N)\] \[P = u1.G \ + \ u2.pk\] \[Prove \ r == P (mod N)\]

Zero-Knowledge Proofs (ZKPs)

  • A method where a prover proves a statement’s truth to a verifier without revealing any details.

Properties

  1. Completeness – If the statement is true, an honest verifier will be convinced.
  2. Soundness – A false statement cannot trick an honest verifier.
  3. Zero-Knowledge – No extra information is revealed except truthfulness.

ZKP Phases

  1. Witness Phase – Prover sends proof.
  2. Challenge Phase – Verifier asks a question.
  3. Response Phase – Prover responds, and the verifier checks validity.

Types of ZKPs

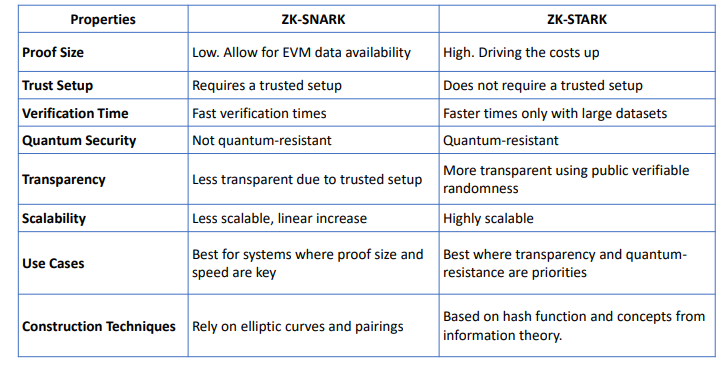
  1. zk-SNARKs –
    • Zero-knowledge Succinct Non-interactive Argument of Knowledge.
    • Zero-Knowledge: No information is revealed except the validity of the statement.
    • Succinct: Proofs are small and fast to verify.
    • Non-Interactive: No back-and-forth interaction between prover and verifier.
    • Argument of Knowledge: The prover convinces the verifier they have knowledge of the statement. - Used in Zcash cryptocurrency for private transactions.
  2. zk-STARKs
    • Zero-Knowledge Scalable Transparent Arguments of Knowledge
    • Designed to overcome limitations of zk-SNARKs.
    • More scalable (handles large computations better).
    • More transparent (does not require a trusted setup).

image.png

Turing Complete

  • A system is Turing Complete if it can simulate a Turing machine, meaning it can execute any computation given enough time and resources.
  • Allows smart contracts to perform complex computations.
  • Ethereum Virtual Machine (EVM) is Turing Complete, meaning it can execute any program.
  • Gas fees prevent infinite loops and excessive computation.
  • Supports decentralized applications (DApps) with flexible logic.

ASIC-Resistant

  • Application-Specific Integrated Circuit: Specialized hardware designed for efficient cryptocurrency mining.
  • ASIC Resistant designed to prevent mining with ASIC devices.
  • Ensures fair mining by making mining feasible for GPU and CPU users.
  • Uses memory-intensive or computationally complex algorithms that reduce ASIC efficiency.
  • Examples: Monero (RandomX), Vertcoin (Lyra2REv3), Ravencoin (KAWPOW).
Sem6, Blockchain
sem6 blockchain
This post is licensed under CC BY 4.0 by the author.